Tứ diện đều là một hình học cơ bản nhưng rất quan trọng trong toán học không gian. Một trong những câu hỏi thú vị liên quan đến hình học này là: Tứ Diện Đều Có Tâm Đối Xứng Không? Để trả lời câu hỏi này,hãy cùng hocvn chúng ta cần hiểu rõ các khía cạnh liên quan đến hình học của tứ diện đều, bao gồm tính đối xứng, tâm, và cách chúng tương tác với nhau.
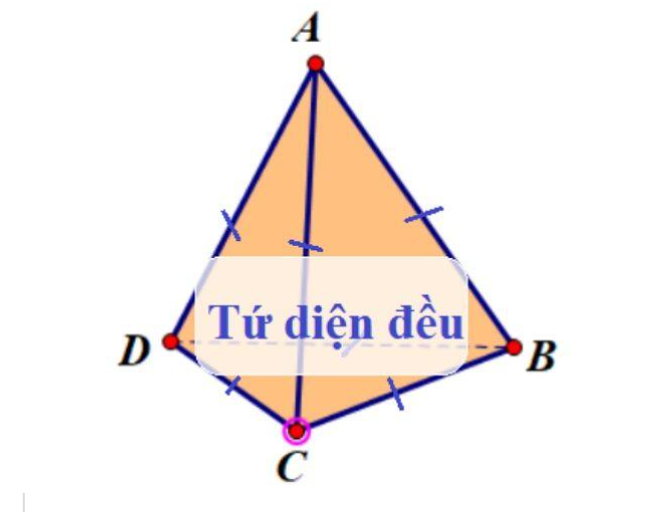
Tứ Diện Đều Là Gì?
Tứ diện đều là một hình đa diện đều với bốn mặt là các tam giác đều. Đặc điểm nổi bật của nó là mỗi mặt, cạnh, và góc đều có kích thước bằng nhau. Tứ diện đều có:
- 4 đỉnh
- 6 cạnh
- 4 mặt là tam giác đều
Tứ diện đều là một trong năm hình đa diện đều (Platonic Solids), cùng với lập phương, bát diện đều, mười hai mặt đều và hai mươi mặt đều.
Tính Đối Xứng Của Tứ Diện Đều
Tính đối xứng là một trong những yếu tố quan trọng khi phân tích một hình học. Tứ diện đều nổi tiếng vì có nhiều loại đối xứng khác nhau. Trong số đó, hai loại phổ biến nhất là đối xứng quay và đối xứng gương.
- Đối xứng quay: Tứ diện đều có các trục quay đi qua tâm của nó, và khi quay một góc nhất định, hình vẫn trùng khớp với chính nó. Điều này là do tính chất đều đặn của hình tam giác đều.
- Đối xứng gương: Tứ diện đều có đối xứng gương qua các mặt phẳng đi qua một đỉnh và tâm của mặt đối diện. Các mặt phẳng này chia hình thành hai phần bằng nhau, tạo nên tính đối xứng gương.
Tuy nhiên, tâm đối xứng lại là một khái niệm khác. Để xác định liệu tứ diện đều có tâm đối xứng hay không, chúng ta cần hiểu rõ hơn về khái niệm tâm trong hình học.
Tâm Của Tứ Diện Đều
Trong hình học, có nhiều loại tâm khác nhau có thể được xác định cho một hình đa diện, bao gồm:
- Trọng tâm: Là điểm cân bằng của một vật thể, được xác định bởi trung bình cộng vị trí các đỉnh.
- Tâm của mặt cầu ngoại tiếp: Là tâm của mặt cầu đi qua tất cả các đỉnh của tứ diện đều.
Tuy nhiên, tâm đối xứng là điểm mà khi ta thực hiện phép đối xứng qua nó, hình vẫn giữ nguyên. Ví dụ, một hình lập phương có tâm đối xứng vì khi đối xứng qua tâm, mọi điểm trên lập phương đều được giữ nguyên vị trí đối xứng tương đương.
Trong trường hợp của tứ diện đều, mặc dù nó có nhiều loại đối xứng khác nhau, nó không có tâm đối xứng. Điều này là do khi thực hiện phép đối xứng qua một điểm bất kỳ trong hoặc ngoài tứ diện đều, không có sự tương ứng chính xác giữa các điểm của nó với nhau.
So Sánh Với Các Hình Đa Diện Đều Khác
Để hiểu rõ hơn về tính đối xứng của tứ diện đều, chúng ta có thể so sánh nó với một số hình đa diện đều khác như lập phương và bát diện đều.
- Lập phương: Lập phương có 6 mặt vuông và có tâm đối xứng rõ ràng. Khi thực hiện đối xứng qua tâm của lập phương, tất cả các đỉnh và mặt đều tương ứng chính xác với nhau. Do đó, lập phương có cả đối xứng quay và tâm đối xứng.
- Bát diện đều: Bát diện đều là hình đa diện đều với 8 mặt tam giác đều. Nó cũng có tính đối xứng quay và đối xứng gương, nhưng giống như tứ diện đều, nó không có tâm đối xứng.
Như vậy, so với các hình đa diện đều khác, tứ diện đều mặc dù có nhiều tính đối xứng nhưng vẫn thiếu một yếu tố quan trọng là tâm đối xứng.
Kết Luận
Qua phân tích các khía cạnh của tứ diện đều, từ tính đối xứng đến vị trí tâm, chúng ta có thể kết luận rằng tứ diện đều không có tâm đối xứng. Tuy nhiên, hình này vẫn giữ vai trò quan trọng trong hình học nhờ tính chất đối xứng quay và gương. Khả năng đối xứng đa dạng của nó khiến tứ diện đều trở thành một đối tượng thú vị trong nghiên cứu và ứng dụng trong nhiều lĩnh vực, từ toán học đến khoa học và kỹ thuật.
Các Ứng Dụng Của Tứ Diện Đều
Tứ diện đều không chỉ là một đối tượng toán học lý thú mà còn có nhiều ứng dụng trong thực tế. Ví dụ, trong khoa học vật liệu, các phân tử hóa học đôi khi có cấu trúc giống tứ diện đều, và trong kỹ thuật, tứ diện đều được ứng dụng để tạo ra các cấu trúc bền vững với tỷ lệ trọng lượng nhẹ.
Hoc vn hy vọng bài viết đã giúp bạn hiểu rõ hơn về tứ diện đều và trả lời câu hỏi liệu Tứ Diện Đều Có Tâm Đối Xứng Không?
Xem thêm:
[HƯỚNG DẪN] Cách Tính Số Đo Góc Lớp 7 Đơn Giản
[GIẢI ĐÁP] Hình Bình Hành Có Trục Đối Xứng Không?