Trong chương trình Vật lý lớp 12, các hàm lượng giác như sin và cos thường xuất hiện khi chúng ta phân tích các bài toán về dao động điều hòa, sóng cơ học, và nhiều hiện tượng vật lý khác. Đôi khi, việc đổi từ hàm sin sang hàm cos (hoặc ngược lại) giúp chúng ta giải quyết các bài toán phức tạp một cách dễ dàng hơn. Dưới đây là hướng dẫn của Hocvn về Cách Đổi Sin Sang Cos Vật Lý 12 , lý do thực hiện phép đổi này, và một số lưu ý quan trọng.

I. Giới thiệu về hàm sin và cos trong vật lý
- Hàm sin và cos trong dao động điều hòa:
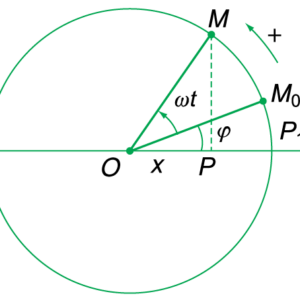
Trong các bài toán dao động điều hòa, các hàm sin và cos được sử dụng để mô tả sự thay đổi của các đại lượng như li độ, vận tốc và gia tốc theo thời gian. Hàm sin và cos biểu diễn các giá trị dao động theo chu kỳ, cho phép mô tả sự dao động qua lại của một vật xung quanh vị trí cân bằng với các yếu tố như biên độ, tần số góc và pha ban đầu.
- Mối liên hệ giữa sin và cos trong toán học:
Toán học đã chỉ ra mối liên hệ chặt chẽ giữa sin và cos qua các công thức lượng giác. Một công thức quan trọng là:
sin(x)=cos(π/2−x)
Công thức này rất hữu ích trong việc chuyển đổi giữa hai hàm lượng giác, đặc biệt trong các bài toán vật lý khi cần đổi từ dạng sin sang cos để dễ dàng so sánh và tính toán.
II. Phương pháp đổi sin sang cos

Sử dụng công thức lượng giác:
Để đổi từ sin sang cos, chúng ta sử dụng các công thức lượng giác cơ bản:
sin(x)=cos(π/2−x) , cos(x)=sin(π/2−x)
Ví dụ: Để đổi hàm sin(ωt) sang dạng cos, chúng ta có:
sin(ωt)=cos(π/2−ωt)
Áp dụng trong các bài toán cụ thể:
Bài toán 1: Tìm pha ban đầu khi đổi sin sang cos:
Giả sử chúng ta có phương trình dao động:
x=Asin(ωt+φ)
Để đổi sang dạng cos, chúng ta sử dụng công thức:
x=Acos(ωt+φ−π/2)
Như vậy, khi chuyển từ sin sang cos, pha ban đầu của dao động thay đổi một lượng −π/2.
III. Lý do đổi sin sang cos trong vật lý

- Tiện lợi trong việc tính toán: Việc chuyển đổi từ sin sang cos hoặc ngược lại giúp dễ dàng so sánh pha của các đại lượng dao động. Trong các bài toán dao động, thường cần xác định các pha để so sánh thời điểm và vị trí của các dao động.
- Dễ dàng trong việc biểu diễn đồ thị: Dùng hàm cos giúp biểu diễn đồ thị dao động một cách nhất quán khi pha ban đầu được đặt ở 0. Điều này giúp đơn giản hóa việc phân tích và xác định các đại lượng trong dao động.
- Ứng dụng trong các bài toán phức tạp: Đổi sin sang cos có thể hữu ích khi giải các bài toán về phương trình dao động, cộng hưởng, hoặc các hiện tượng vật lý phức tạp khác. Nó giúp việc sử dụng công thức và các biến đổi lượng giác trở nên thuận tiện hơn.
IV. Lưu ý khi đổi sin sang cos
- Xác định đúng pha ban đầu: Khi đổi từ sin sang cos, cần phải điều chỉnh pha ban đầu để đảm bảo tính chính xác. Pha ban đầu phải được điều chỉnh thêm hoặc bớt π2frac{pi}{2}2π (hoặc 90 độ) tùy vào hàm được chuyển đổi.
- Hiểu rõ bối cảnh bài toán: Trước khi đổi hàm, cần hiểu rõ bối cảnh và yêu cầu của bài toán để chọn dạng hàm phù hợp. Đổi sai dạng hàm có thể dẫn đến sai lầm trong việc giải quyết bài toán.
- Tránh nhầm lẫn với các công thức khác: Khi thực hiện các phép biến đổi lượng giác, cần chú ý đến các công thức liên quan và tránh nhầm lẫn, đặc biệt khi sử dụng các phép đổi pha hoặc tính toán phức tạp.
Kết luận
Cách Đổi Sin Sang Cos Vật Lý 12 không chỉ giúp giải các bài toán một cách tiện lợi hơn mà còn giúp dễ dàng biểu diễn các đại lượng dao động và phân tích đồ thị. Tuy nhiên, khi thực hiện phép đổi này, cần chú ý đến pha ban đầu, hiểu rõ bối cảnh bài toán và tránh nhầm lẫn với các công thức khác. Nắm vững phương pháp Hocvn đã chia sẻ sẽ giúp học sinh giải quyết tốt hơn các bài toán vật lý lớp 12 liên quan đến dao động và sóng.
Xem thêm:
[TÌM HIỂU] Điều Kiện Để Xảy Ra Phản Xạ Toàn Phần
[HƯỚNG DẪN] Cách Đấu Motor 1 Pha 2 Tụ Chuẩn Nhất