Giới thiệu về hệ trục tọa độ
Trong toán học, hệ trục tọa độ đóng vai trò nền tảng để xác định vị trí các điểm trong không gian hai chiều và ba chiều. Hầu hết học sinh đều bắt đầu làm quen với hệ trục này khi học về hình học hay đại số ở cấp 2. Tuy nhiên, có một câu hỏi thường xuyên được đặt ra trong quá trình học: trục tung là X hay Y? Đây là một trong những nhầm lẫn phổ biến nhưng hoàn toàn có thể giải thích một cách đơn giản.
Trục tọa độ Descartes gồm hai thành phần chính: trục hoành (X) và trục tung (Y). Chúng giao nhau tại một điểm đặc biệt gọi là gốc tọa độ, ký hiệu là (0,0). Mỗi điểm trong mặt phẳng được xác định bởi cặp số (x, y), trong đó x thể hiện vị trí theo chiều ngang còn y biểu thị vị trí theo chiều dọc.
Vậy điều gì khiến chúng ta hay nhầm lẫn giữa hai trục này? Vì sao lại có khái niệm trục hoành và trục tung thay vì chỉ đơn giản gọi là trục X và trục Y? Tất cả sẽ được giải đáp trong bài viết này, cùng với nhiều sự thật thú vị khác mà bạn có thể chưa từng biết đến.
Hệ tọa độ Descartes là gì?
Hệ tọa độ Descartes, hay còn gọi là hệ tọa độ vuông góc, là một phát minh của nhà toán học và triết học người Pháp René Descartes vào thế kỷ 17. Trước đó, các nhà toán học thường vẽ hình học một cách trực quan, nhưng chưa có hệ thống ký hiệu rõ ràng để biểu diễn mối quan hệ giữa hình học và số học. Nhờ Descartes, chúng ta có thể biểu diễn hình học bằng các phương trình số học, tạo tiền đề cho sự phát triển mạnh mẽ của đại số và giải tích sau này.
Trong hệ tọa độ Descartes hai chiều, có hai trục vuông góc với nhau:
- Trục hoành (trục X): nằm ngang.
- Trục tung (trục Y): nằm dọc.
Hai trục này giao nhau tại điểm gốc tọa độ (0,0), từ đó chia mặt phẳng thành bốn góc phần tư. Hệ tọa độ này không chỉ dùng trong toán học mà còn trong nhiều lĩnh vực khác như vật lý, tin học, thiết kế kỹ thuật, và địa lý.
Tìm hiểu trục X và trục Y
Để hiểu được trục tung là X hay Y, ta cần nắm rõ vai trò và vị trí của từng trục:
- Trục X (trục hoành) đại diện cho chiều ngang. Khi tọa độ thay đổi theo X, điểm sẽ di chuyển sang trái hoặc phải.
- Trục Y (trục tung) đại diện cho chiều dọc. Khi giá trị Y tăng, điểm đi lên; khi Y giảm, điểm đi xuống.
Trong biểu đồ toán học, chúng ta thường vẽ trục X trước (theo chiều ngang), sau đó mới vẽ trục Y (theo chiều dọc). Cách sắp xếp này được áp dụng nhất quán trên toàn cầu và trở thành chuẩn mực trong giáo dục.
Vì vậy, trục tung là trục Y, chứ không phải X. Tuy nhiên, nếu bạn chỉ nhìn vào các chữ cái mà không hiểu rõ ý nghĩa, rất dễ bị nhầm lẫn. Đó là lý do vì sao câu hỏi “trục tung là X hay Y” vẫn còn khiến nhiều học sinh bối rối.
Gốc tọa độ: Nơi mọi thứ bắt đầu
Mọi điểm trong hệ tọa độ đều bắt đầu từ gốc tọa độ – vị trí có giá trị (0,0). Đây là nơi hai trục giao nhau và đóng vai trò làm điểm tham chiếu để xác định vị trí các điểm khác.
Ví dụ:
- Điểm A (3, 4) nghĩa là: từ gốc tọa độ, bạn đi 3 đơn vị sang phải (theo trục X) và 4 đơn vị lên trên (theo trục Y).
- Ngược lại, điểm B (-2, -5) là đi 2 đơn vị sang trái và 5 đơn vị xuống dưới.
Sự kết hợp giữa hai trục tạo nên khả năng mô tả chính xác mọi vị trí trong mặt phẳng, dù là trong toán học, bản đồ hay các phần mềm vẽ kỹ thuật như AutoCAD hay Photoshop.
“Trục tung” có nghĩa là gì?
Trong tiếng Việt, “trục tung” mang nghĩa “đường thẳng thẳng đứng”. Từ “tung” thể hiện chiều đứng lên, rơi xuống, trái ngược với “hoành” – nghĩa là nằm ngang, trải ra theo chiều ngang.
Trong bối cảnh toán học:
- Trục hoành: là trục nằm ngang, tương ứng với trục X.
- Trục tung: là trục thẳng đứng, tương ứng với trục Y.
Từ ngữ Việt Nam rất giàu hình ảnh. Bạn có thể tưởng tượng như thế này: chữ “Y” giống như một cái cây mọc thẳng đứng từ mặt đất lên – đó chính là trục tung. Trong khi đó, chữ “X” như cánh tay dang ngang – chính là trục hoành.
Vai trò của trục tung trong toán học
Trong nhiều bài toán, đặc biệt là giải phương trình hay vẽ đồ thị hàm số, trục tung giữ vai trò thể hiện giá trị đầu ra – thường là biến phụ thuộc (thường gọi là y). Đây là nơi mà bạn sẽ quan sát xem hàm số tăng hay giảm, lên đỉnh hay xuống đáy.
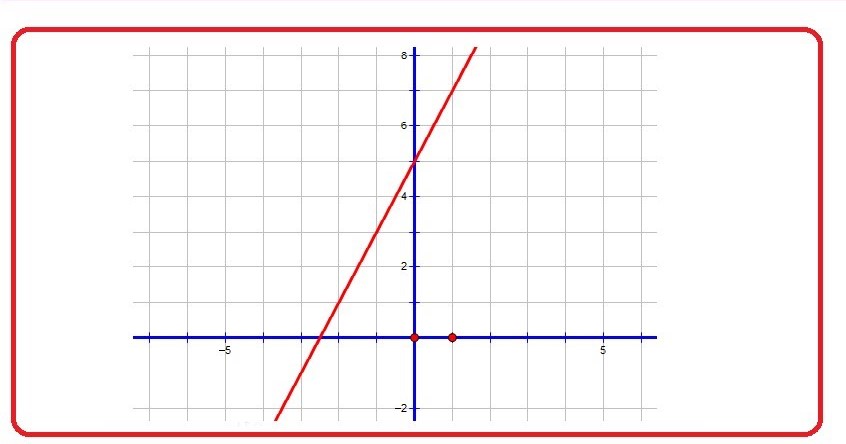
Ví dụ, khi bạn vẽ đồ thị hàm số y = 2x + 1, thì:
- x là giá trị bạn nhập vào.
- y là kết quả được tính ra và thể hiện trên trục tung.
Chính vì vậy, nếu bạn vẽ sai trục, thì toàn bộ đồ thị có thể sẽ bị lệch hoặc sai hoàn toàn – ảnh hưởng đến việc hiểu đúng bản chất của hàm số.
Phân biệt trục tung và trục hoành
| Đặc điểm | Trục Tung (Y) | Trục Hoành (X) |
|---|---|---|
| Chiều | Thẳng đứng | Nằm ngang |
| Biểu thị | Biến phụ thuộc (thường là y) | Biến độc lập (thường là x) |
| Ý nghĩa | Lên – xuống | Trái – phải |
| Từ khóa | “tung” = đứng thẳng | “hoành” = nằm ngang |
| Vị trí trong mặt phẳng | Dọc theo trục đứng | Dọc theo trục ngang |
Nếu bạn ghi nhớ bảng so sánh này, bạn sẽ không bao giờ bị nhầm lẫn giữa trục tung là X hay Y nữa!
Giải đáp thắc mắc: Trục tung là X hay Y?
Và đây chính là phần trọng tâm của toàn bộ bài viết – lời giải rõ ràng và dứt khoát cho câu hỏi “trục tung là X hay Y”.
Câu trả lời đúng: Trục tung là Y.
Tất cả tài liệu, sách giáo khoa, phần mềm đồ thị, công cụ toán học, và tiêu chuẩn quốc tế đều quy ước rằng:
- X là trục hoành (chiều ngang).
- Y là trục tung (chiều dọc).
Tuy nhiên, điều đáng chú ý là nhiều học sinh Việt Nam bị nhầm do cách gọi tên theo nghĩa Hán-Việt. Khi không nắm vững quy ước ban đầu, việc nhầm X là trục tung hoàn toàn có thể xảy ra.
Mẹo ghi nhớ nhanh:
“Tung thì bay lên trời → Trục Y.”
“Hoành như tay dang ngang → Trục X.”

Lịch sử phát triển hệ tọa độ
Để hiểu rõ hơn vì sao trục tung là trục Y, chúng ta cần nhìn lại lịch sử hình thành của hệ trục tọa độ – một công cụ toán học đã thay đổi cách loài người tư duy về không gian và phép đo.
René Descartes và sự ra đời của hệ tọa độ
Vào năm 1637, René Descartes đã xuất bản một tác phẩm mang tên La Géométrie, trong đó ông giới thiệu ý tưởng kết hợp hình học và đại số – một phát minh được xem là nền tảng cho toán học hiện đại.
Ông đã đề xuất việc dùng hai đường vuông góc để biểu diễn vị trí các điểm trên mặt phẳng: một đường nằm ngang và một đường thẳng đứng. Để dễ biểu diễn, ông sử dụng các chữ cái x và y làm ký hiệu cho các giá trị tương ứng theo chiều ngang và dọc.
Điều thú vị là trục X luôn được ưu tiên trước khi đề cập đến trục Y. Cách viết tọa độ cũng phản ánh điều này: (x, y) – giá trị x được nhắc đến trước.
Từ đó về sau, hệ tọa độ Descartes nhanh chóng trở thành chuẩn mực giảng dạy ở khắp nơi trên thế giới, và trục Y – trục tung chính thức được ghi nhận trong tất cả các tài liệu học thuật.
Thuật ngữ trong toán học Việt Nam và toàn cầu
Ở Việt Nam, ta sử dụng các từ ngữ Hán-Việt: “trục hoành” (nằm ngang) và “trục tung” (đứng thẳng). Trong khi đó, các quốc gia khác như Mỹ, Anh, Pháp… đơn giản gọi là X-axis (trục X) và Y-axis (trục Y).
Việc dùng các từ Hán-Việt có thể gây đôi chút khó hiểu nếu người học không được giảng giải kỹ, dẫn đến câu hỏi “trục tung là X hay Y” trở nên phổ biến trong các lớp học.
Trực quan hóa trục tung trong đời sống hàng ngày
Dù học toán có vẻ trừu tượng, nhưng trục tung (Y) thật ra hiện diện rất nhiều trong cuộc sống xung quanh chúng ta. Hãy cùng khám phá những ứng dụng thực tế:
Đồ thị trong giáo dục và kinh doanh
- Trong học đường, khi học sinh vẽ đồ thị hàm số, trục tung biểu diễn giá trị kết quả đầu ra.
- Trong các bài thí nghiệm vật lý, trục Y thường thể hiện đại lượng đo được (vận tốc, nhiệt độ, lực…).
- Trong kinh doanh, biểu đồ cột, biểu đồ đường dùng trục tung để hiển thị doanh thu, sản lượng, lợi nhuận theo thời gian (trục X).
Ví dụ: Biểu đồ thể hiện tăng trưởng doanh thu từng quý:
- Trục X: Quý 1, Quý 2, Quý 3, Quý 4
- Trục Y: Số tiền (đơn vị: triệu đồng)
Ứng dụng thực tế: Từ định vị GPS đến kiến trúc
- Trong hệ thống GPS, các vị trí được mã hóa bằng hệ tọa độ địa lý. Mỗi điểm có tọa độ tương tự như (x, y), và trục tung tương ứng với vĩ độ (latitude) – chiều đi lên hoặc xuống trái đất.
- Trong kiến trúc, khi thiết kế bản vẽ mặt đứng, chiều cao của công trình thường được biểu diễn theo trục Y.
Qua những ví dụ trên, ta thấy rằng trục tung (trục Y) là yếu tố không thể thiếu trong mọi lĩnh vực đời sống, từ học thuật đến công nghệ, kỹ thuật và kinh doanh.
Thực hành toán học với trục tung
Giờ ta sẽ tìm hiểu cách áp dụng trục tung vào thực hành toán học, đặc biệt trong việc vẽ đồ thị, xác định tọa độ điểm và giải bài toán không gian.
Cách xác định đúng điểm trên trục Y
Một điểm nằm trên trục tung sẽ có giá trị x = 0. Ví dụ:
- Điểm M (0, 5) → nằm trên trục Y, cách gốc tọa độ 5 đơn vị theo chiều dọc.
- Điểm N (0, -3) → nằm dưới gốc tọa độ, cách 3 đơn vị.
Công thức ghi nhớ: Nếu x = 0, thì điểm đó nằm trên trục Y.
Công cụ vẽ đồ thị và phần mềm hỗ trợ
Bạn có thể sử dụng các công cụ sau để luyện tập:
- GeoGebra – phần mềm trực quan, miễn phí, hỗ trợ học toán từ lớp 6 đến đại học.
- Desmos – ứng dụng vẽ đồ thị online đơn giản và đẹp mắt.
- Microsoft Excel hoặc Google Sheets – tạo biểu đồ bằng số liệu thực tế.
Những phần mềm này đều hỗ trợ thể hiện rõ trục X và trục Y, giúp bạn hiểu chính xác trục tung là Y, tránh nhầm lẫn.
Phương trình đường thẳng dọc theo trục Y
Đường thẳng song song với trục tung có dạng x = a, trong khi đường thẳng nằm dọc trên trục Y sẽ có dạng:
- y = mx + b (với m là hệ số góc, b là giao điểm với trục Y).
Cách xác định giao điểm với trục tung cũng rất đơn giản: bạn chỉ cần thay x = 0 vào phương trình.
Ví dụ: y = 3x + 2 → Giao điểm trục tung tại y = 2.
Vai trò của trục tung trong vật lý và kỹ thuật
Không chỉ trong toán học, trục tung còn xuất hiện thường xuyên trong vật lý học và kỹ thuật công trình.
Chuyển động theo phương thẳng đứng
- Trong bài toán rơi tự do, vật thể chỉ chuyển động theo trục tung (Y).
- Phương trình vật lý thường có dạng: s = v₀t + ½gt², với s là độ cao – thể hiện dọc theo trục Y.
Phân tích lực và vector
- Khi phân tích lực tác động lên vật, ta tách ra thành lực theo trục X và lực theo trục Y.
- Biểu đồ lực (free-body diagram) luôn thể hiện lực trọng trường (trọng lượng) hướng xuống – theo trục Y.
Việc hiểu rõ trục tung là Y giúp học sinh giải đúng các bài toán về gia tốc, chuyển động, lực tác động và phương pháp vector.
Chiến lược giáo dục giúp học sinh ghi nhớ trục tung
Việc học và ghi nhớ trục tung là Y không khó, nhưng để học sinh không nhầm lẫn, giáo viên và phụ huynh cần áp dụng các phương pháp học tập phù hợp với tư duy trực quan và ngôn ngữ.
Mẹo ghi nhớ chức năng của các trục
Một số mẹo học đơn giản giúp học sinh dễ dàng nhớ rằng trục tung là trục Y, ví dụ:
- “Tung bay lên trời” – hình ảnh cho chiều dọc, gắn với trục Y.
- “Hoành tráng nằm ngang” – dễ liên tưởng tới trục X nằm ngang.
Ngoài ra, học sinh có thể dùng sơ đồ hình ảnh hoặc vẽ sơ đồ màu để ghi nhớ lâu hơn.
Câu thần chú học nhanh và dễ hiểu
Các thầy cô có thể dạy học sinh học qua thơ hoặc thần chú như sau:
“Trục hoành là X ngang ngang,
Trục tung là Y dọc thẳng hàng trên cao.”
Hoặc:
“X nằm ngang, Y đứng dọc,
Đồ thị không sai – học thật giỏi!”
Những sai lầm thường gặp và cách khắc phục
- Nhầm thứ tự tọa độ (x, y): học sinh thường viết ngược lại như (y, x), dẫn đến xác định sai vị trí.
- Đổi trục khi vẽ đồ thị: nhiều em đảo trục mà không biết, gây ra kết quả sai.
Giải pháp:
Thường xuyên luyện tập vẽ đồ thị đơn giản, sử dụng giấy kẻ ô ly, và kiểm tra xem giá trị nào thuộc X, giá trị nào thuộc Y.
Cách học sinh Việt Nam hiểu về trục tung
Khảo sát thực tế từ các lớp học phổ thông
Theo khảo sát nhỏ tại một số trường THCS, có đến 46% học sinh lớp 7 và 8 từng nhầm lẫn giữa trục tung và trục hoành. Phần lớn nguyên nhân đến từ:
- Thiếu ví dụ trực quan.
- Không hiểu nghĩa của từ “tung” và “hoành”.
- Ghi nhớ máy móc mà không hiểu bản chất.
Ảnh hưởng của ngôn ngữ đến việc học toán
Ngôn ngữ Hán – Việt có phần trang trọng và khó hiểu hơn với học sinh nhỏ tuổi. Nhiều em không rõ “tung” và “hoành” nghĩa là gì, từ đó dẫn đến nhầm lẫn trong khi làm bài.
Giải pháp hiệu quả:
- Sử dụng từ ngữ hiện đại như “trục X (nằm ngang)” và “trục Y (thẳng đứng)” song song với từ gốc.
- Ứng dụng hình ảnh minh họa, hoạt hình, trò chơi để giúp trẻ hiểu khái niệm một cách tự nhiên hơn.
Công nghệ hỗ trợ học hệ trục tọa độ
Với sự phát triển của công nghệ, học sinh ngày nay có thể học về trục tung – trục Y một cách dễ hiểu và sinh động hơn rất nhiều.
Ứng dụng và trò chơi tương tác
Các ứng dụng như:
- Kahoot, Quizizz: tạo câu đố phân biệt X và Y nhanh chóng, thú vị.
- GeoGebra: cho phép học sinh kéo thả điểm trên hệ tọa độ và thấy ngay vị trí thay đổi.
- Desmos: học vẽ đồ thị theo từng bước đơn giản, hỗ trợ tiếng Việt.
Thực tế tăng cường giúp củng cố kiến thức
Một số phần mềm thực tế tăng cường (AR) như Merge Cube, CoSpaces Edu cho phép học sinh nhìn thấy hệ tọa độ 3D trong không gian thực, giúp các em hình dung rõ trục X – Y – Z, từ đó củng cố chắc chắn kiến thức về trục tung là Y.
Sự khác biệt trong cách gọi tên trục ở các quốc gia
Cách các nước gọi trục X và Y
- Hoa Kỳ & Anh: sử dụng “X-axis” và “Y-axis”.
- Pháp: “axe des abscisses” (trục X), “axe des ordonnées” (trục Y).
- Nhật Bản: dùng trực tiếp X軸 (X-jiku) và Y軸 (Y-jiku).
Dù cách gọi khác nhau, mọi quốc gia đều quy định trục Y là trục tung – trục thẳng đứng.
Tác động đến việc dạy và học toán toàn cầu
Hệ thống giáo dục Việt Nam thường sử dụng thuật ngữ cổ điển. Nếu so sánh với chương trình quốc tế như IB hoặc Cambridge, cách tiếp cận thường dùng ký hiệu trực tiếp (X, Y) giúp học sinh ít bị rối hơn.
Câu hỏi thường gặp về trục tung là X hay Y
1. Vì sao học sinh thường nhầm lẫn trục tung với trục hoành?
Do cách gọi bằng Hán – Việt thiếu minh họa thực tế. Học sinh dễ nhầm khi học máy móc, không hiểu rõ ý nghĩa.
2. Có cách nào dễ nhớ để phân biệt không?
Có! Hãy nhớ: “Tung thì bay lên → là trục Y”, và “Hoành nằm ngang → là trục X”.
3. Trục tung luôn là Y trong mọi biểu đồ?
Đúng. Trong hệ tọa độ Descartes chuẩn, trục tung luôn là Y, không đổi trừ khi có chỉ định đặc biệt.
4. Có trường hợp nào trục X là trục tung không?
Rất hiếm. Chỉ xảy ra trong các biểu đồ đặc biệt (ví dụ xoay đồ thị), nhưng mặc định luôn là: trục tung = Y.
5. Trục tung có quan trọng trong các môn ngoài toán không?
Có. Trong vật lý, địa lý, công nghệ, thiết kế – trục tung giúp xác định vị trí, chiều cao, độ sâu, lực…
6. Làm sao để luyện vẽ đồ thị nhanh và chính xác?
Thường xuyên luyện tập bằng phần mềm như GeoGebra, Desmos, Excel. Vẽ tay bằng giấy kẻ ô cũng rất hiệu quả.
Kết luận và lời khuyên dành cho người học
Qua bài viết, hocvn và các bạn đã giải đáp trọn vẹn câu hỏi “trục tung là X hay Y” – một thắc mắc tưởng chừng đơn giản nhưng lại rất phổ biến.
Khẳng định lại: Trục tung là trục Y – luôn là đường thẳng đứng trong hệ tọa độ vuông góc.
Hiểu rõ điều này không chỉ giúp học sinh làm bài tốt hơn mà còn hỗ trợ họ trong các môn học khác như vật lý, công nghệ, địa lý, lập trình…
Lời khuyên cuối cùng:
- Đừng học thuộc lòng một cách máy móc.
- Hãy học bằng hình ảnh, ví dụ, trò chơi, và ứng dụng thực tế.
- Luôn luyện tập vẽ, xác định tọa độ, sử dụng công cụ hỗ trợ.
Nếu bạn ghi nhớ mẹo “Tung thì thẳng đứng → Y”, thì câu hỏi “trục tung là X hay Y” sẽ không bao giờ khiến bạn bối rối nữa!
Xem thêm:
[HƯỚNG DẪN] Rút Gọn Phân Số 11/22
[GIẢI ĐÁP] 7hm 3dam Bằng Bao Nhiêu M?