Chứng Minh Đường Song Song Với Mặt Phẳng là một bài toán quan trọng trong hình học không gian. Bài toán này không chỉ yêu cầu sự hiểu biết về các khái niệm cơ bản mà còn đòi hỏi sự vận dụng linh hoạt các phương pháp chứng minh và định lý hình học. Trong bài viết này, hãy cùng hoc vn tìm hiểu các khái niệm cốt lõi, các phương pháp chứng minh phổ biến và những ứng dụng thực tế của nó.
1. Khái Niệm Cơ Bản
Trước khi đi sâu vào các phương pháp chứng minh, chúng ta cần nắm vững một số khái niệm cơ bản về đường thẳng và mặt phẳng trong không gian.
- Đường thẳng: Trong hình học, đường thẳng là tập hợp các điểm nằm trên một hàng và kéo dài vô tận về hai phía. Đường thẳng không có điểm bắt đầu và kết thúc.
- Mặt phẳng: Mặt phẳng là một bề mặt phẳng kéo dài vô tận theo mọi hướng. Trong không gian ba chiều, mặt phẳng có thể được xác định bởi ba điểm không thẳng hàng.
Quan hệ giữa đường thẳng và mặt phẳng: Đường thẳng có thể nằm trên mặt phẳng, cắt mặt phẳng tại một điểm, hoặc không giao với mặt phẳng. Trường hợp đặc biệt khi đường thẳng không cắt mặt phẳng và không nằm trên mặt phẳng, đường thẳng đó song song với mặt phẳng.
2. Tiêu Chuẩn và Định Lý Về Đường Song Song Với Mặt Phẳng
Tiêu chuẩn để một đường thẳng song song với mặt phẳng là: Đường thẳng đó không cắt mặt phẳng, hoặc tất cả các điểm của đường thẳng đều cách đều mặt phẳng tại mọi vị trí.
Định lý Euclid về song song trong hình học không gian khẳng định rằng: “Nếu một đường thẳng không giao với một mặt phẳng và song song với một đường thẳng khác nằm trên mặt phẳng đó, thì đường thẳng ban đầu sẽ song song với mặt phẳng”.
3. Phương Pháp Chứng Minh
Có nhiều phương pháp khác nhau để chứng minh một đường thẳng song song với một mặt phẳng. Dưới đây là một số phương pháp phổ biến:
Phương pháp vector:
- Trong phương pháp này, chúng ta sử dụng các vector chỉ phương của đường thẳng và mặt phẳng. Nếu vector chỉ phương của đường thẳng song song với vector chỉ phương của một đường thẳng trên mặt phẳng mà không có điểm chung, chúng ta có thể kết luận rằng đường thẳng đó song song với mặt phẳng.
Phương pháp tọa độ:
- Với phương pháp này, chúng ta biểu diễn đường thẳng và mặt phẳng dưới dạng phương trình tọa độ trong không gian ba chiều. Nếu tọa độ của đường thẳng và mặt phẳng không có nghiệm chung (tức là chúng không giao nhau), đường thẳng được chứng minh là song song với mặt phẳng.
Sử dụng định lý Euclid:
- Dựa vào định lý Euclid, ta có thể chứng minh đường thẳng song song với mặt phẳng bằng cách chỉ ra rằng đường thẳng này song song với một đường thẳng khác nằm trên mặt phẳng.
4. Ví Dụ và Bài Tập Thực Tiễn
Để hiểu rõ hơn về các phương pháp trên, hãy xem xét ví dụ sau:
Ví dụ: Cho đường thẳng ddd không nằm trong mặt phẳng (P)(P)(P) và đường thẳng aaa nằm trong mặt phẳng (P)(P)(P). Nếu ddd song song với aaa, thì đường thẳng ddd cũng sẽ song song với mặt phẳng (P)(P)(P).
Bài tập: Chứng minh rằng một đường thẳng ddd song song với mặt phẳng (P)(P)(P) nếu đường thẳng đó không cắt bất kỳ điểm nào trên mặt phẳng (P)(P)(P).
5. Ứng Dụng Thực Tiễn
Chứng minh đường thẳng song song với mặt phẳng không chỉ là một bài toán lý thuyết mà còn có nhiều ứng dụng thực tế:
- Trong kiến trúc và xây dựng: Khi thiết kế các tòa nhà hoặc cầu cạn, việc đảm bảo các đường thẳng và mặt phẳng song song là cực kỳ quan trọng để duy trì tính ổn định và cân đối của cấu trúc.
- Trong thiết kế đồ họa: Để tạo ra các bản vẽ 3D chính xác, các nhà thiết kế cần phải đảm bảo rằng các đường song song với các mặt phẳng khác nhau, từ đó tạo ra sự phối cảnh chính xác.
6. Mở Rộng Chủ Đề
Ngoài việc chứng minh đường thẳng song song với mặt phẳng, chúng ta còn có thể nghiên cứu thêm về các định lý song song trong không gian và định lý đường thẳng cắt mặt phẳng. Những định lý này cung cấp nền tảng lý thuyết sâu rộng hơn về mối quan hệ giữa các đối tượng hình học trong không gian ba chiều.
7. Hình Ảnh Minh Họa
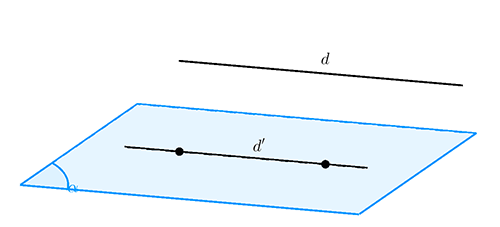
Hình ảnh minh họa về cách chứng minh đường thẳng song song với mặt phẳng có thể giúp bạn dễ dàng hình dung các phương pháp đã được đề cập. Dưới đây là một sơ đồ đơn giản:
- Sơ đồ đường thẳng ddd và mặt phẳng (P)(P)(P) với ví dụ cụ thể về phương pháp vector.
- Hình ảnh mô phỏng ứng dụng của đường song song trong không gian kiến trúc.
Kết Luận
Việc chứng minh đường song song với mặt phẳng không chỉ là một vấn đề lý thuyết mà còn có giá trị ứng dụng rộng rãi trong nhiều lĩnh vực thực tiễn. Bằng cách nắm vững các khái niệm cơ bản và sử dụng linh hoạt các phương pháp chứng minh, chúng ta có thể dễ dàng áp dụng kiến thức hình học vào đời sống và công việc.
Hocvn hy vọng vơi bài viết trên không chỉ giải quyết vấn đề về Chứng Minh Đường Song Song Với Mặt Phẳng mà còn đưa ra các ứng dụng và bài tập thực tiễn, giúp người đọc hiểu sâu hơn về chủ đề này.
Xem thêm:
[HƯỚNG DẪN] Cách Vẽ Đồ Thị Hàm Số Y Ax B (y = ax + b)
[HƯỚNG DẪN] Cách Tính Sai Số Tuyệt Đối Toán 10