Định Nghĩa Cơ Bản Về Tam Giác Đều
a. Tam giác đều là gì?
Trước khi trả lời câu hỏi: “Hình Tam Giác Đều Có Tâm Đối Xứng Không?”, chúng ta phải biết hình tam giác như thế nào?
Tam giác đều là một trong những loại hình tam giác cơ bản nhất trong hình học phẳng. Đây là tam giác có ba cạnh bằng nhau và ba góc trong đều bằng 60 độ. Nhờ vào sự đồng đều này, tam giác đều được xem là hình học hoàn hảo và cân bằng nhất trong số các loại tam giác.
Không chỉ có tính đối xứng rõ ràng, tam giác đều còn là nền tảng cho nhiều hình học khác và được ứng dụng trong toán học, vật lý, kỹ thuật, và thậm chí là nghệ thuật.
b. Các đặc điểm hình học của tam giác đều
Tam giác đều có một số đặc điểm rất đặc biệt:
- Ba cạnh bằng nhau
- Ba góc bằng nhau (mỗi góc 60°)
- Có ba trục đối xứng đi qua đỉnh và trung điểm cạnh đối diện
- Có trọng tâm, tâm nội tiếp, tâm ngoại tiếp, và trực tâm trùng nhau
Tính chất đặc biệt này làm cho tam giác đều trở nên độc đáo khi so sánh với các loại tam giác khác như tam giác cân hay tam giác thường.
c. Ứng dụng thực tế của tam giác đều trong cuộc sống
Tam giác đều không chỉ là một khái niệm trong sách giáo khoa. Chúng xuất hiện trong:
- Kiến trúc: Nhiều mái nhà, cầu thang, hoặc họa tiết đều sử dụng hình tam giác đều để tăng tính thẩm mỹ và độ bền.
- Kỹ thuật: Trong cơ học, tam giác đều được dùng trong kết cấu chịu lực do phân bố lực đồng đều.
- Thiết kế đồ họa: Tam giác đều được sử dụng để tạo sự cân bằng và hài hòa trong bố cục.
Tâm Đối Xứng Là Gì Trong Hình Học?
a. Định nghĩa tâm đối xứng
Tâm đối xứng là một khái niệm quan trọng trong hình học phẳng. Một hình được gọi là có tâm đối xứng nếu tồn tại một điểm sao cho mỗi điểm của hình, khi quay quanh điểm đó một góc 180 độ, sẽ đi đến một điểm khác cũng thuộc hình. Nói cách khác, nếu ta lấy một điểm bất kỳ trong hình và phản chiếu nó qua tâm, ta sẽ nhận được một điểm đối xứng tương ứng cũng nằm trong hình.
Ví dụ rõ ràng nhất là hình tròn hoặc hình vuông – cả hai đều có tâm đối xứng rõ ràng. Đối với những hình này, tâm của chúng cũng chính là tâm đối xứng.
b. Ví dụ minh họa đơn giản
Một số ví dụ thường gặp về các hình có tâm đối xứng bao gồm:
- Hình tròn: Tâm của đường tròn chính là tâm đối xứng vì mọi điểm trên đường tròn đều đối xứng với một điểm khác thông qua tâm.
- Hình vuông: Có tâm đối xứng là giao điểm của hai đường chéo.
- Hình chữ nhật: Tương tự như hình vuông, giao điểm của hai đường chéo là tâm đối xứng.
Trong khi đó, tam giác nói chung không phải lúc nào cũng có tâm đối xứng, và đây chính là điểm mấu chốt khi xem xét câu hỏi “hình tam giác đều có tâm đối xứng không”.
c. Vai trò của tâm đối xứng trong phân tích hình học
Trong toán học, tâm đối xứng giúp:
- Xác định tính chất hình học: Giúp suy luận các điểm tương ứng mà không cần đo đạc.
- Tối ưu hóa tính toán: Trong kỹ thuật và thiết kế CAD, tâm đối xứng giúp tạo các bản thiết kế cân bằng và tiết kiệm thời gian.
- Tăng khả năng kiểm tra và chứng minh: Hỗ trợ trong việc xây dựng và kiểm chứng định lý hình học.
Quan Hệ Giữa Tam Giác Đều Và Tâm Đối Xứng
a. Phân tích lý thuyết
Về lý thuyết, tam giác đều có nhiều dạng đối xứng, đặc biệt là đối xứng trục và đối xứng quay. Tuy nhiên, để xác định xem tam giác đều có tâm đối xứng hay không, ta cần phân biệt rõ giữa đối xứng tâm và đối xứng trục/quay.
- Tam giác đều có ba trục đối xứng, mỗi trục đi qua một đỉnh và trung điểm cạnh đối diện.
- Tam giác đều có đối xứng quay quanh trọng tâm một góc 120 độ và 240 độ.
- Tuy nhiên, đối xứng tâm đòi hỏi mọi điểm phải có ảnh đối xứng qua một điểm duy nhất – điều này không đúng với tam giác đều.
b. Dẫn chứng thực nghiệm
Hãy thử dùng phần mềm như GeoGebra để kiểm tra:
- Vẽ một tam giác đều.
- Đặt điểm trọng tâm (nơi giao nhau của ba đường trung tuyến).
- Lấy một điểm bất kỳ trên một cạnh.
- Phản chiếu điểm đó qua trọng tâm – điểm kết quả không nằm trên tam giác.
Kết luận: trọng tâm không phải là tâm đối xứng của tam giác đều.
c. Tính chất liên kết giữa hình và tâm đối xứng
Điều thú vị là mặc dù tam giác đều rất cân đối, nhưng không có tâm đối xứng. Điều này làm nổi bật tính phức tạp và tinh tế của hình học phẳng. Tính đối xứng của tam giác đều là đối xứng theo ba trục, nhưng không có một điểm cố định nào phản chiếu toàn bộ hình theo đúng định nghĩa tâm đối xứng.
Vẽ Tam Giác Đều Và Xác Định Tâm Đối Xứng
a. Các bước vẽ chính xác tam giác đều
Để vẽ một tam giác đều chính xác, bạn cần thực hiện như sau:
- Vẽ một đoạn thẳng AB có độ dài cho trước.
- Dùng compa với bán kính AB, quay một đường cung từ điểm A.
- Tiếp tục dùng compa từ điểm B, cùng bán kính AB, quay đường cung cắt cung trước tại điểm C.
- Nối A–C và B–C để hoàn tất tam giác đều ABC.
b. Cách xác định tâm hình học
Trong tam giác đều:
- Trọng tâm là giao điểm của ba đường trung tuyến.
- Tâm đường tròn ngoại tiếp cũng là trọng tâm.
- Tâm đường tròn nội tiếp cũng trùng điểm này.
Điều này tạo cảm giác “có tâm”, nhưng như đã nói, đó không phải là tâm đối xứng theo định nghĩa nghiêm ngặt.
c. Vị trí và đặc điểm của tâm trong tam giác đều
Tâm hình học trong tam giác đều có các đặc điểm sau:
- Nằm chính giữa tam giác.
- Là tâm quay của tam giác với các góc 120°, 240°, và 360°.
- Là nơi hội tụ của:
- Trọng tâm
- Tâm nội tiếp
- Tâm ngoại tiếp
- Trực tâm
Dù có nhiều điểm hội tụ đặc biệt, nhưng vẫn không phải là tâm đối xứng, vì không đáp ứng điều kiện đối xứng hình học toàn phần.
Tâm Của Các Loại Tam Giác Khác Nhau
a. Tam giác cân và tâm đối xứng
Tam giác cân có một trục đối xứng, nhưng cũng không có tâm đối xứng. Điều này có nghĩa là việc phản chiếu một điểm bất kỳ qua điểm nào trong tam giác cân không tạo ra một điểm đối xứng tương ứng thuộc hình.
b. Tam giác thường và sự thiếu vắng tâm đối xứng
Tam giác thường không có cạnh bằng nhau, góc không đều nhau, và không có bất kỳ trục hay tâm đối xứng nào. Đây là hình thiếu tính đối xứng nhất trong các tam giác.
c. So sánh với tam giác đều
So với tam giác cân và tam giác thường, tam giác đều vượt trội về tính đối xứng trục và đối xứng quay, nhưng cũng không đủ điều kiện để có tâm đối xứng.
Tam Giác Đều Có Bao Nhiêu Tâm?
Tam giác đều đặc biệt ở chỗ tất cả các loại “tâm” trong tam giác đều trùng nhau:
a. Trọng tâm (Centroid)
- Giao điểm của ba đường trung tuyến.
- Luôn nằm trong tam giác.
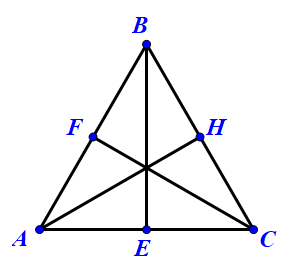
b. Tâm đường tròn nội tiếp (Incenter)
- Giao điểm của ba phân giác.
- Là tâm của đường tròn nội tiếp.
c. Tâm đường tròn ngoại tiếp (Circumcenter)
- Giao điểm của ba đường trung trực.
- Là tâm của đường tròn đi qua ba đỉnh.
d. Tâm trực tâm (Orthocenter)
- Giao điểm của ba đường cao.
- Trong tam giác đều, trực tâm = trọng tâm = tâm nội tiếp = tâm ngoại tiếp.
Tuy nhiên, dù có đủ các loại tâm trên, tam giác đều không có tâm đối xứng theo định nghĩa hình học cổ điển.
Hình Tam Giác Đều Có Tâm Đối Xứng Không?
a. Giải thích bằng hình học phẳng
Để trả lời câu hỏi “hình tam giác đều có tâm đối xứng không?”, ta cần hiểu lại định nghĩa một cách chính xác.
Như đã phân tích ở phần trên, tâm đối xứng là một điểm mà khi mọi điểm trên hình được đối xứng qua đó, chúng ta thu được chính hình ban đầu.
Trong hình tròn hay hình vuông, bất kỳ điểm nào trên hình khi đối xứng qua tâm đều có ảnh nằm trên cùng một hình. Nhưng trong tam giác đều:
- Khi lấy một điểm bất kỳ trên một cạnh và đối xứng nó qua trọng tâm (điểm thường bị nhầm là tâm đối xứng), ta không nhận được một điểm nằm trên tam giác.
- Do đó, không tồn tại điểm nào thỏa mãn điều kiện là tâm đối xứng cho tam giác đều.
=> Kết luận: Tam giác đều KHÔNG có tâm đối xứng.
b. Dẫn chứng từ trục đối xứng
Tam giác đều có ba trục đối xứng đi qua mỗi đỉnh và trung điểm của cạnh đối diện. Khi gập hình theo trục đó, hai phần của tam giác sẽ trùng khớp.
Tuy nhiên, đối xứng trục không đồng nghĩa với đối xứng tâm. Đối xứng tâm yêu cầu phải có một điểm duy nhất mà từ đó mọi điểm được phản chiếu qua sẽ nằm trên hình — điều này không xảy ra với tam giác đều.
Dẫn chứng này càng củng cố cho câu trả lời phủ định: tam giác đều không có tâm đối xứng.
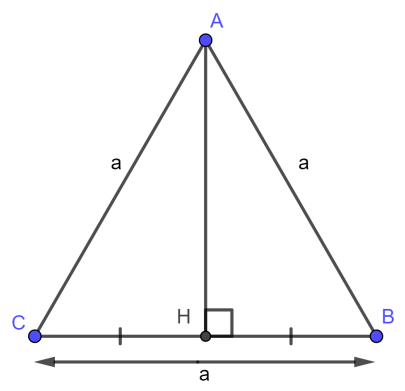
c. So sánh với hình học khác có tâm đối xứng
| Hình học | Tâm đối xứng | Đối xứng trục | Đối xứng quay |
|---|---|---|---|
| Hình tròn | Có | Vô hạn | Vô hạn |
| Hình vuông | Có | 4 trục | Có (90°, 180°, …) |
| Hình chữ nhật | Có | 2 trục | Có (180°) |
| Tam giác đều | Không | 3 trục | Có (120°, 240°) |
Bảng trên cho thấy: dù tam giác đều có cả đối xứng trục và quay, nhưng vẫn không đủ điều kiện để có tâm đối xứng, không giống như hình tròn hay hình vuông.
Lý Do Tại Sao Tam Giác Đều Không Có Tâm Đối Xứng
a. Đặc tính đối xứng quay vs. đối xứng tâm
Một lỗi phổ biến khi học hình học là nhầm lẫn giữa đối xứng quay và đối xứng tâm.
- Đối xứng quay nghĩa là hình có thể được xoay quanh một điểm (trong trường hợp này là trọng tâm) một góc nhất định (ví dụ 120°, 240°) và vẫn trùng khớp với chính nó.
- Đối xứng tâm nghĩa là mọi điểm đều có một điểm đối xứng tương ứng nằm trong hình, khi phản chiếu qua tâm.
Tam giác đều có đối xứng quay, nhưng lại thiếu điều kiện cần cho đối xứng tâm.
b. Sai lầm phổ biến khi xác định tâm đối xứng
Học sinh thường nhầm lẫn các điểm đặc biệt như:
- Trọng tâm
- Tâm ngoại tiếp
- Tâm nội tiếp
- Trực tâm
là tâm đối xứng. Thật ra, đây là những điểm đặc biệt không phải tâm đối xứng, vì phản chiếu một điểm qua chúng không đảm bảo điểm kết quả nằm trong hình.
Ví dụ:
- Lấy điểm giữa một cạnh, phản chiếu qua trọng tâm: điểm đối xứng sẽ nằm bên ngoài hình.
- Như vậy, không thể xem đó là tâm đối xứng.
c. Trường hợp ngoại lệ có thể tồn tại?
Có một số trường hợp học sinh tạo ra các hình “giống tam giác đều” bằng cách sắp xếp ba đoạn thẳng với sự hỗ trợ của phần mềm. Trong các tình huống lý tưởng hóa, họ lầm tưởng rằng hình có tâm đối xứng.
Tuy nhiên, dưới góc độ hình học chính xác, và theo định nghĩa toán học, tam giác đều không bao giờ có tâm đối xứng.
Vai Trò Của Đối Xứng Trong Thiết Kế Và Kiến Trúc
a. Ứng dụng tam giác đều
Trong thực tế, tam giác đều có mặt ở nhiều nơi:
- Kiến trúc cổ điển: mái nhà hình tam giác giúp phân tán trọng lực đều.
- Kết cấu xây dựng: các khung tam giác đều trong giàn mái, cầu treo, hay giàn giáo có tính chịu lực tốt.
- Biểu tượng học: nhiều biểu tượng tôn giáo, văn hóa dùng tam giác đều do tính cân bằng của nó.
b. Đối xứng trong mỹ thuật và thiết kế
Tam giác đều thường dùng để tạo sự hài hòa thị giác:
- Trong thiết kế logo: ví dụ, logo Google Drive là tập hợp ba tam giác đều xoay quanh một tâm.
- Trong mỹ thuật: tam giác đều dùng làm bố cục cân đối cho tranh vẽ, ảnh chụp.
Dù không có tâm đối xứng, tam giác đều vẫn mang lại cảm giác cân bằng mạnh mẽ.
c. Hiểu đúng về hình học để ứng dụng hiệu quả
Nếu hiểu đúng rằng tam giác đều không có tâm đối xứng, người thiết kế sẽ:
- Tránh các sai lầm trong việc sắp xếp đối xứng hình ảnh.
- Tối ưu hóa bố cục theo trục đối xứng, thay vì dựa vào giả định sai về tâm đối xứng.
- Ứng dụng hiệu quả trong mô phỏng 3D, thiết kế hình học, và lập trình đồ họa.
Cách Giảng Dạy Khái Niệm Này Cho Học Sinh Cấp 2
a. Ví dụ minh họa bằng mô hình
Giáo viên có thể sử dụng mô hình giấy như sau:
- Cắt tam giác đều bằng giấy.
- Gập hình theo trục đi qua đỉnh và trung điểm cạnh đối diện để minh họa đối xứng trục.
- Thử gập theo điểm giữa tam giác để minh họa không tồn tại tâm đối xứng.
=> Giúp học sinh hiểu bằng trực quan thay vì chỉ qua định nghĩa.
b. Dùng phần mềm hình học như GeoGebra
Sử dụng phần mềm:
- Vẽ tam giác đều.
- Đặt điểm trọng tâm.
- Dùng công cụ “đối xứng qua điểm” để kiểm tra.
- So sánh với hình tròn hoặc vuông để nhận ra sự khác biệt.
Phương pháp này hiện đại, sinh động và dễ tiếp thu.
c. Bài tập luyện tập kèm lời giải
Một số bài tập ví dụ:
- Bài 1: Vẽ tam giác đều, xác định trọng tâm, thực hiện đối xứng một điểm bất kỳ.
- Bài 2: So sánh hình tròn, hình vuông, hình tam giác đều về mặt tâm đối xứng.
- Bài 3: Tìm tất cả các trục đối xứng của tam giác đều.
Lời giải kèm theo sẽ giúp học sinh tự kiểm tra và hiểu sâu hơn.
So Sánh Hình Tam Giác Với Các Hình Khác Có Tâm Đối Xứng
a. Hình vuông
Hình vuông có đầy đủ các loại đối xứng:
- 4 trục đối xứng (2 đường chéo và 2 đường trung trực).
- 1 tâm đối xứng là giao điểm hai đường chéo.
- Đối xứng quay 90°, 180°, 270°, và 360°.
So với tam giác đều, hình vuông vượt trội về mặt đối xứng, đặc biệt là có tâm đối xứng thật sự.
b. Hình tròn
Hình tròn là “vua” của đối xứng:
- Vô số trục đối xứng đi qua tâm.
- Tâm đối xứng chính là tâm hình tròn.
- Đối xứng quay vô hạn: quay bất kỳ góc nào cũng vẫn trùng với chính nó.
Điều này làm nổi bật điểm hạn chế của tam giác đều – tuy có nhiều trục đối xứng và đối xứng quay, nhưng vẫn không có tâm đối xứng.
c. Hình chữ nhật
Hình chữ nhật có:
- 2 trục đối xứng qua hai đường trung trực.
- Tâm đối xứng là giao điểm của hai đường chéo.
- Đối xứng quay 180°.
Tuy đơn giản hơn hình vuông, hình chữ nhật vẫn có tâm đối xứng – điều mà tam giác đều không sở hữu.
Câu Hỏi Trắc Nghiệm Về Tam Giác Đều Và Tâm Đối Xứng
a. Câu hỏi lý thuyết
Câu 1: Tam giác đều có bao nhiêu trục đối xứng?
A. 1
B. 2
C. 3
D. Không có
Đáp án: C
Câu 2: Tam giác đều có tâm đối xứng không?
A. Có
B. Không
C. Chỉ khi các cạnh bằng nhau
D. Tùy hình vẽ
Đáp án: B
b. Câu hỏi vận dụng
Câu 3: Khi phản chiếu một điểm trên tam giác đều qua trọng tâm, điểm mới nằm ở đâu?
A. Trong tam giác
B. Ngoài tam giác
C. Ở cạnh đối diện
D. Ở trung điểm đường cao
Đáp án: B
c. Giải thích đáp án
Các đáp án đều dựa trên tính chất hình học đã phân tích:
- Tam giác đều có 3 trục đối xứng.
- Không có điểm nào thỏa mãn định nghĩa tâm đối xứng.
- Phản chiếu qua trọng tâm không giữ nguyên vị trí trong hình.
Quan Điểm Sai Lệch Và Lý Giải Hợp Lý
a. Những lầm tưởng thường gặp
- “Tam giác đều có tâm đối xứng vì cân đối quá!”
Sai – không thỏa mãn điều kiện đối xứng tâm. - “Trọng tâm cũng là tâm đối xứng.”
Sai – chỉ là điểm giao nhau của các đường đặc biệt.
b. Lý do tâm đối xứng bị hiểu sai
Nguyên nhân chính:
- Nhầm lẫn giữa đối xứng trục, đối xứng quay, và đối xứng tâm.
- Sự trùng nhau của các điểm đặc biệt trong tam giác đều khiến người học nhầm tưởng có tâm đối xứng.
c. Cách tiếp cận để học đúng từ đầu
- Dạy bằng hình ảnh, mô hình thực tế.
- Dùng phần mềm minh họa rõ ràng.
- Làm bài tập phản chiếu điểm để “thấy tận mắt” sự khác biệt.
Kết Luận Khoa Học Từ Hình Học Cổ Điển Đến Hiện Đại
a. Tam giác đều trong toán học cổ đại
Từ thời Hy Lạp cổ đại, tam giác đều đã được xem là biểu tượng của sự hoàn hảo:
- Dùng trong nghệ thuật, kiến trúc.
- Là nền tảng của nhiều mô hình toán học.
b. Hiện đại hóa và vai trò trong công nghệ
Ngày nay, tam giác đều xuất hiện trong:
- Thiết kế cơ khí (kết cấu chịu lực).
- Lập trình máy tính (mô hình đồ họa 3D).
- Trí tuệ nhân tạo (học hình học không gian).
c. Liên hệ với các nguyên lý hình học hiện đại
Trong hình học hiện đại, việc phân biệt rõ các loại đối xứng là rất quan trọng. Tâm đối xứng không thể xác định chỉ dựa vào “cảm giác cân đối” – cần đúng định nghĩa và dẫn chứng hình học.
Câu Hỏi Thường Gặp (FAQs)
a. Tam giác đều có bao nhiêu trục đối xứng?
Tam giác đều có 3 trục đối xứng, mỗi trục đi qua một đỉnh và trung điểm cạnh đối diện.
b. Có thể coi tâm của tam giác đều là tâm đối xứng không?
Không. Dù trọng tâm là điểm đặc biệt, nhưng nó không phải là tâm đối xứng theo định nghĩa hình học.
c. Tại sao tam giác đều không có tâm đối xứng như hình tròn?
Vì phản chiếu điểm bất kỳ qua trọng tâm không luôn tạo ra điểm nằm trong tam giác, nên không thỏa mãn định nghĩa tâm đối xứng.
d. Các phần mềm nào giúp học sinh xác định tâm đối xứng?
Phần mềm như GeoGebra, Cabri Geometry, và Desmos là công cụ hữu hiệu để trực quan hóa khái niệm đối xứng.
e. Tam giác nào có tâm đối xứng?
Không có tam giác nào có tâm đối xứng. Chỉ các hình như hình tròn, vuông, chữ nhật, lục giác đều… mới có.
f. Có thể dùng tam giác đều để dạy khái niệm đối xứng không?
Có thể dạy về đối xứng trục và đối xứng quay, nhưng không nên dùng để minh họa đối xứng tâm.
Kết Luận
a. Tóm tắt câu trả lời
Qua phân tích chi tiết, hocvn khẳng định: hình tam giác đều KHÔNG có tâm đối xứng. Dù hình rất cân đối, có nhiều tính chất đặc biệt, nhưng vẫn không thỏa mãn điều kiện đối xứng tâm.
b. Tầm quan trọng của hiểu đúng kiến thức cơ bản
Việc hiểu đúng về các khái niệm hình học như đối xứng trục, quay và tâm đối xứng giúp:
- Tránh sai lầm khi giải bài.
- Tăng khả năng áp dụng vào thực tế.
- Tạo nền tảng vững chắc cho toán học cao cấp.
c. Kêu gọi tiếp tục khám phá thế giới hình học
Hình học không chỉ là một môn học – nó là cách chúng ta nhìn thế giới xung quanh. Khi hiểu đúng bản chất của hình, bạn sẽ thấy được vẻ đẹp trong logic, sự cân đối trong nghệ thuật, và tính toán học trong thiên nhiên.
Hãy tiếp tục học hỏi, khám phá – bởi vì toán học là ngôn ngữ bí ẩn tuyệt đẹp của vũ trụ!
Xem thêm:
Ma Trận Khả Nghịch Khi Nào? Khám Phá Điều Kiện & Phương Pháp Xác Định
[GIẢI ĐÁP] Hai Vecto Ngược Hướng Thì Như Thế Nào?